Transformaciones lineales

Qué es una transformación lineal?

R/. Una transformación lineal es una función. Cómo toda función tiene su dominio y condominio, sólo que éstos son espacios vectoriales. Para que exista una transformación lineal, se deben cumplir varias propiedades entre dos vectores.

Cuáles son las condiciones para que exista un transformación lineal

R/. Condición 1: T(u+v)=T(u)+T(v)∀u,v∈V

Condición 2: T(k.v)=k.T(v)∀v∈V,∀k∈R

Al menos cinco propiedades o teoremas de las transformaciones lineales

R/. 1. La imagen del vector nulo del dominio 0V0V es el vector nulo del codominio 0w0w.

2. La imagen del vector –v–v es igual al opuesto de la imagen de v

3. Consideremos rr vectores del espacio vectorial VV

4. T: V ® W es un monomorfismo si, y sólo si, T es inyectiva. Es decir, T es un monomorfismo si y sólo si ” u, v Î V: T(u) = T(v) Þ u = v.

5.T: V ® W es un epimorfismo si, y sólo si, T es sobreyectiva. Es decir, T es un epimorfismo si y sólo si ” w Î W, $ v Î V / w = T(v).

6.T: V ® W es un isomorfismo si, y sólo si, T es biyectiva. Es decir, T es un isomorfismo si y sólo si es un monomorfismo y un epimorfismo.

7.T: V ® W es un endomorfismo si y sólo si V = W.

8.T: V ® W es un automorfismo si y sólo si T es un isomorfismo y un endomorfismo.

Un ejemplo de una transformación lineal y Cómo probar esa transformación lineal.

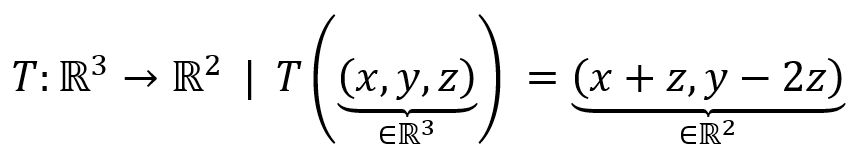
Condición 1: T(u+v)=T(u)+T(v)∀u,v∈VT(u+v)=T(u)+T(v)∀u,v∈V

Tomemos dos vectores de R3R3

u=(u1,u2,u3)u=(u1,u2,u3)

v=(v1,v2,v3)v=(v1,v2,v3)

Veamos si

T(u+v)=T(u)+T(v)T(u+v)=T(u)+T(v)

Primero hacemos la suma de uu y vv:

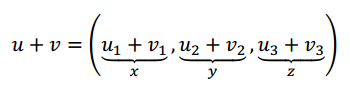Y ahora aplicamos TT:

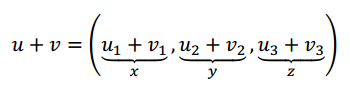
T(u+v)=(u1+v1+u3+v3,u2+v2–2u3–2v3)T(u+v)=(u1+v1+u3+v3,u2+v2–2u3–2v3)

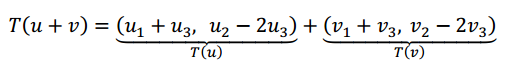
T(u+v)=T(u)+T(v)T(u+v)=T(u)+T(v)

En conclusión: se cumple la primera de las condiciones.

Nos faltaría la otra propiedad.

Condición 2:

T(k.v)=k.T(v)∀v∈V,∀k∈RT(k.v)=k.T(v)∀v∈V,∀k∈R

T(k.v)=T((kv1,kv2,kv3))=(kv1+kv3,kv2–2kv3)T(k.v)=T((kv1,kv2,kv3))=(kv1+kv3,kv2–2kv3)

=k.(v1+v3,v2–2v3)=k.T(v)=k.(v1+v3,v2–2v3)=k.T(v)

Como TT cumple las dos condiciones, es una transformación lineal.